首页 论坛 创客及开源专区 开源、DIY及3D打印 STM32控制 MPU6050 六轴陀螺仪-资料汇总
STM32控制 MPU6050 六轴陀螺仪-资料汇总
技术交流群:123768874
一、 MPU6050简介
MPU6050是一种非常流行的空间运动传感器芯片,可以获取器件当前的三个加速度分量和三个旋转角速度。由于其体积小巧,功能强大,精度较高,不仅被广泛应用于工业,同时也是航模爱好者的神器,被安装在各类飞行器上驰骋蓝天。
MPU6050的数据是有较大噪音的,若不进行滤波会对整个控制系统的精准确带来严重影响。MPU6050芯片内自带了一个数据处理子模块DMP,已经内置了滤波算法,在许多应用中使用DMP输出的数据已经能够很好的满足要求。

我们感兴趣的数据位于0x3B到0x48这14个字节的寄存器中。这些数据会被动态更新,更新频率最高可达1000HZ。下面列出相关寄存器的地址,数据的名称。注意,每个数据都是2个字节。
0x3B,加速度计的X轴分量ACC_X0x3D,加速度计的Y轴分量ACC_Y
0x3F,加速度计的Z轴分量ACC_Z
0x41,当前温度TEMP
0x43,绕X轴旋转的角速度GYR_X
0x45,绕Y轴旋转的角速度GYR_Y
0x47,绕Z轴旋转的角速度GYR_Z
MPU6050芯片的座标系是这样定义的:令芯片表面朝向自己,将其表面文字转至正确角度,此时,以芯片内部中心为原点,水平向右的为X轴,竖直向上的为Y轴,指向自己的为Z轴。见下图:
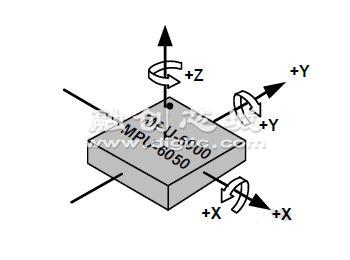
我们只关心加速度计和角速度计数据的含义,下面分别介绍。
2.1 加速度计
加速度计的三轴分量ACC_X、ACC_Y和ACC_Z均为16位有符号整数,分别表示器件在三个轴向上的加速度,取负值时加速度沿座标轴负向,取正值时沿正向。
三个加速度分量均以重力加速度g的倍数为单位,能够表示的加速度范围,即倍率可以统一设定,有4个可选倍率:2g、4g、8g、16g。以ACC_X为例,若倍率设定为2g(默认),则意味着ACC_X取最小值-32768时,当前加速度为沿X轴正方向2倍的重力加速度;若设定为4g,取-32768时表示沿X轴正方向4倍的重力加速度,以此类推。显然,倍率越低精度越好,倍率越高表示的范围越大,这要根据具体的应用来设定。
2.2 角速度计
绕X、Y和Z三个座标轴旋转的角速度分量GYR_X、GYR_Y和GYR_Z均为16位有符号整数。从原点向旋转轴方向看去,取正值时为顺时针旋转,取负值时为逆时针旋转。
三个角速度分量均以“度/秒”为单位,能够表示的角速度范围,即倍率可统一设定,有4个可选倍率:250度/秒、500度/秒、1000度/秒、2000度/秒。以GYR_X为例,若倍率设定为250度/秒,则意味着GYR取正最大值32768时,当前角速度为顺时针250度/秒;若设定为500度/秒,取32768时表示当前角速度为顺时针500度/秒。显然,倍率越低精度越好,倍率越高表示的范围越大。
在读取加速度计和角速度计的数据并换算为物理值后,根据不同的应用,数据有不同的解译方式。本章将以飞行器运动模型为例,根据加速度和角速度来算出当前的飞行姿态。
3.1 加速度计模型
我们可以把加速度计想象为一个正立方体盒子里放着一个球,这个球被弹簧固定在立方体的中心。当盒子运动时,根据假想球的位置即可算出当前加速度的值。想象如果在太空中,盒子没有任何受力时,假想球将处于正中心的位置,三个轴的加速度均为0。见下图:

如果我们给盒子施加一个水平向左的力,那么显然盒子就会有一个向左的加速度,此时盒内的假想球会因为惯性作用贴向盒内的右侧面。如下图所示:

了保证数据的物理意义,MPU6050的加速度计是以假想球在三轴上座标值的相反数作为三个轴的加速度值。当假想球的位置偏向一个轴的正向时,该轴的加速度读数为负值,当假想球的位置偏向一个轴的负向时,该轴的加速度读数为正值。
根据以上分析,当我们把MPU6050芯片水平放于地方,芯片表面朝向天空,此时由于受到地球重力的作用, 假想球的位置偏向Z轴的负向,因此Z轴的加速度读数应为正,且在理想情况下应为g。注意,此加速度的物理意义并不是重力加速度,而是自身运动的加速度,可以这样理解:正因为其自身运动的加速度与重力加速度大小相等方向相反,芯片才能保持静止。
3.2 Roll-pitch-yaw模型与姿态计算
表示飞行器当前飞行姿态的一个通用模型就是建立下图所示坐标系,并用Roll表示绕X轴的旋转,Pitch表示绕Y轴的旋转,Yaw表示绕Z轴的旋转。

由于MPU6050可以获取三个轴向上的加速度,而地球重力则是长期存在且永远竖直向下,因此我们可以根据重力加速度相对于芯片的指向为参考算得当前姿态。
为方便起见,我们让芯片正面朝下固定在上图飞机上,且座标系与飞机的坐标系完全重合,以三个轴向上的加速度为分量,可构成加速度向量a(x,y,z)。假设当前芯片处于匀速直线运动状态,那么a应垂直于地面上向,即指向Z轴负方向,模长为|a|=g=\sqrt{x^2+y^2+z^2}(与重力加速度大小相等,方向相反,见3.1节)。若芯片(座标系)发生旋转,由于加速度向量a仍然竖直向上,所以Z轴负方向将不再与a重合。见下图。
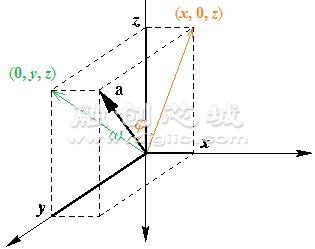
为了方便表示,上图坐标系的Z轴正方向(机腹以及芯片正面)向下,X轴正方向(飞机前进方向)向右。此时芯片的Roll角\phi(黄色)为加速度向量与其在XZ平面上投影(x,0,z)的夹角,Pitch角\omega(绿色)与其在YZ平面上投影(0,y,z)的夹角。求两个向量的夹角可用点乘公式:a \cdot b=|a|\cdot|b|\cdot\cos\theta ,简单推导可得:
\phi=\cos^{-1}(\sqrt{x^2+z^2}/g),以及\omega=\cos^{-1}(\sqrt{y^2+z^2}/g)
注意,因为arccos函数只能返回正值角度,因此还需要根据不同情况来取角度的正负值。当y值为正时,Roll角要取负值,当x轴为负时,Pitch角要取负值。
3.3 Yaw角的问题
因为没有参考量,所以无法求出当前的Yaw角的绝对角度,只能得到Yaw的变化量,也就是角速度GYR_Z。当然,我们可以通过对GYR_Z积分的方法来推算当前Yaw角(以初始值为准),但由于测量精度的问题,推算值会发生漂移,一段时间后就完全失去意义了。然而在大多数应用中,比如无人机,只需要获得GRY_Z就可以了。
如果必须要获得绝对的Yaw角,那么应当选用MPU9250这款九轴运动跟踪芯片,它可以提供额外的三轴罗盘数据,这样我们就可以根据地球磁场方向来计算Yaw角了,具体方法此处不再赘述。
四、数据处理与实现
MPU6050芯片提供的数据夹杂有较严重的噪音,在芯片处理静止状态时数据摆动都可能超过2%。除了噪音,各项数据还会有偏移的现象,也就是说数据并不是围绕静止工作点摆动,因此要先对数据偏移进行校准 ,再通过滤波算法消除噪音。
4.1 校准
校准是比较简单的工作,我们只需要找出摆动的数据围绕的中心点即可。我们以GRY_X为例,在芯片处理静止状态时,这个读数理论上讲应当为0,但它往往会存在偏移量,比如我们以10ms的间隔读取了10个值如下:
-158.4, -172.9, -134.2, -155.1, -131.2, -146.8, -173.1, -188.6, -142.7, -179.5
这10个值的均值,也就是这个读数的偏移量为-158.25。在获取偏移量后,每次的读数都减去偏移量就可以得到校准后的读数了。当然这个偏移量只是估计值,比较准确的偏移量要对大量的数据进行统计才能获知,数据量越大越准,但统计的时间也就越慢。一般校准可以在每次启动系统时进行,那么你应当在准确度和启动时间之间做一个权衡。
三个角速度读数GYR_X、GYR_Y和GYR_Z均可通过统计求平均的方法来获得,但三个加速度分量就不能这样简单的完成了,因为芯片静止时的加速度并不为0。
4.2 卡尔曼滤波
对于夹杂了大量噪音的数据,卡尔曼滤波器的效果无疑是最好的。如果不想考虑算法细节,可以直接使用Arduino的Klaman Filter库完成。在我们的模型中,一个卡尔曼滤波器接受一个轴上的角度值、角速度值以及时间增量,估计出一个消除噪音的角度值。跟据当前的角度值和上一轮估计的角度值,以及这两轮估计的间隔时间,我们还可以反推出消除噪音的角速度。
资料截图



 回复
回复
 举报
举报
-

- 0000000000000000
-
1888 发帖7917 回复34980 积分
- 私信他 +关注
-

- 76e0df1c572e4f5
-
0 发帖5 回复110 积分
- 私信他 +关注
块
导
航
举报
请选择举报类别
- 广告垃圾
- 违规内容
- 恶意灌水
- 重复发帖


 发帖
发帖
 回复
回复




 楼主
楼主